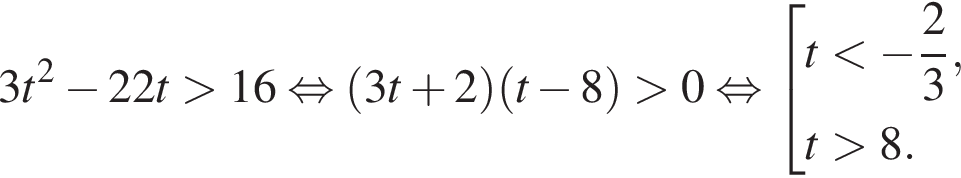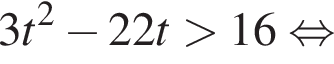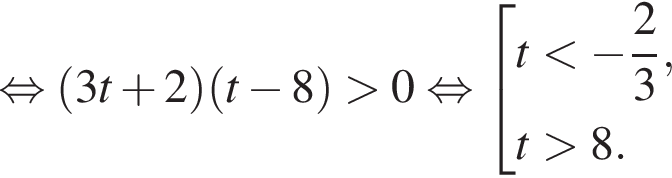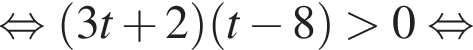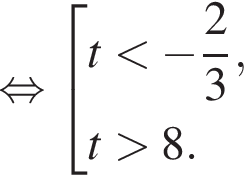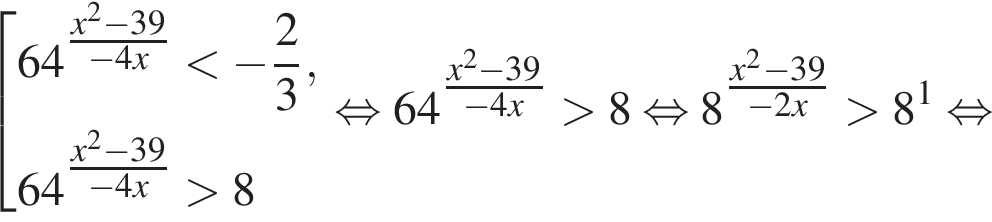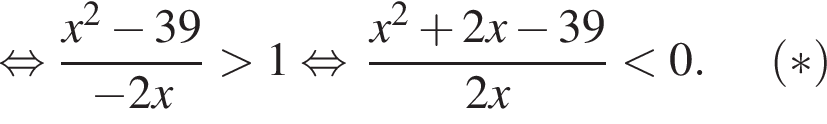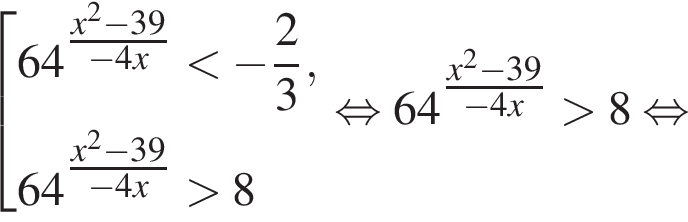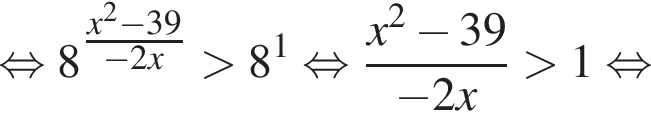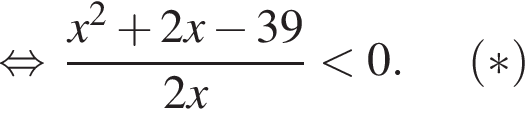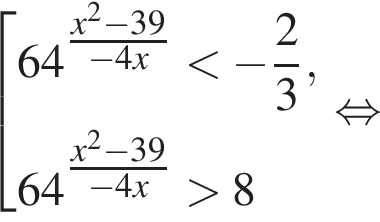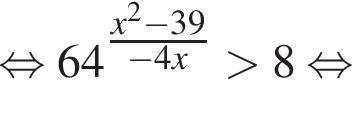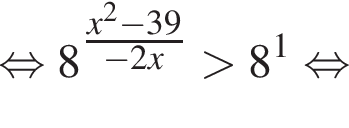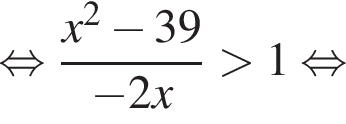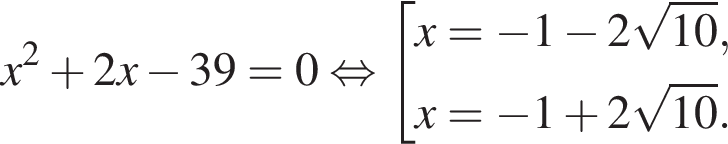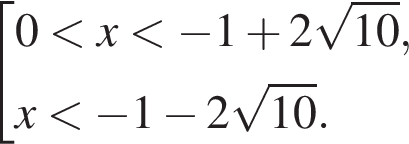1. Задание № 1610 

Сложность: III
Классификатор алгебры: 4\.2\. Неравенства первой и второй степени относительно показательных функций
Методы алгебры: Замена переменной
Показательные неравенства
i
Найдите произведение наибольшего целого отрицательного и наибольшего целого положительного решений неравенства
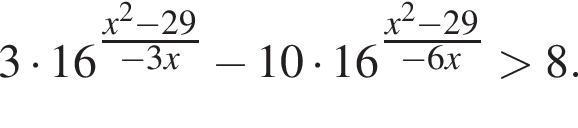
Решение. Заметим, что неравенство является квадратным относительно показательной функции:
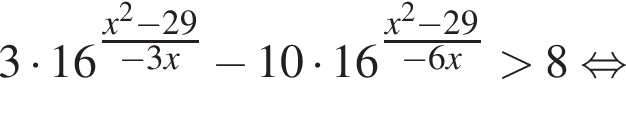
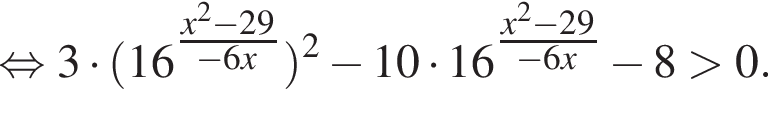
Примем 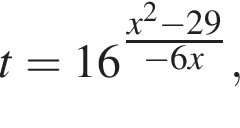 тогда имеем:
тогда имеем:
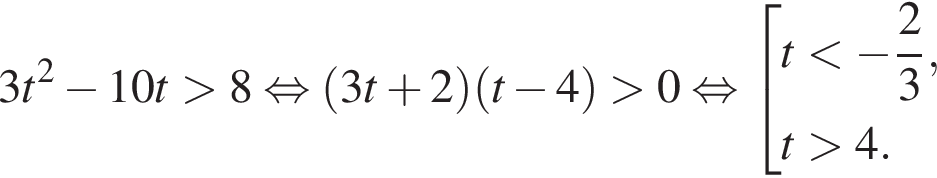
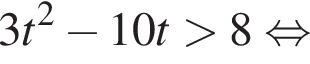
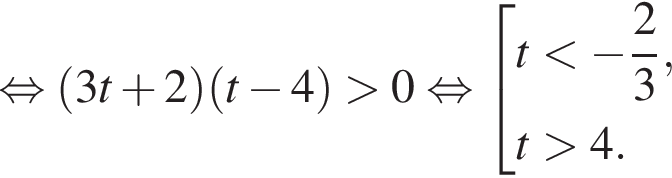
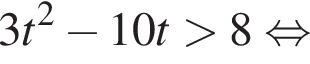
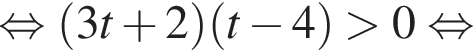
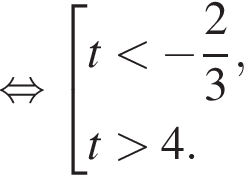
Вернёмся к исходной переменной, получим:
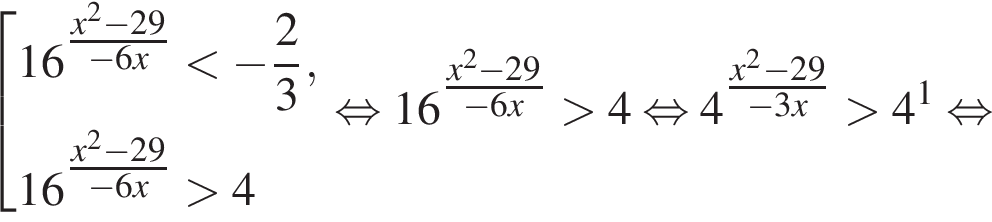
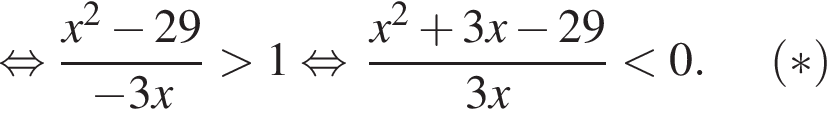
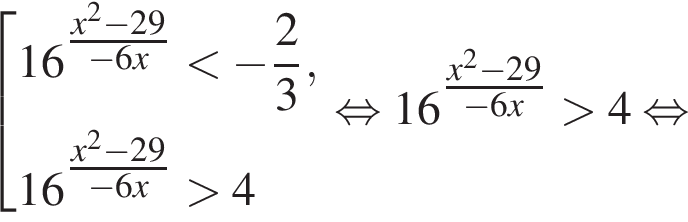
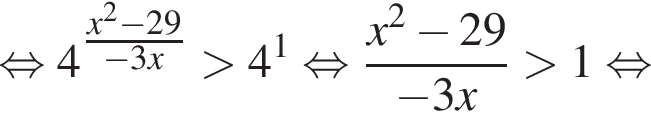
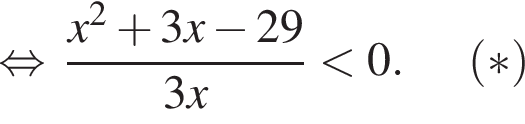
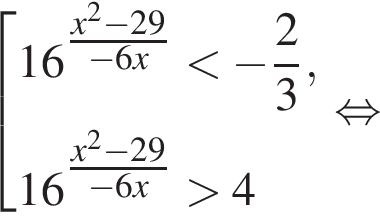
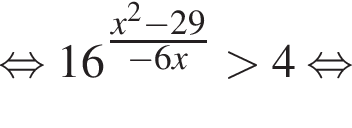
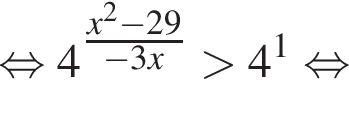
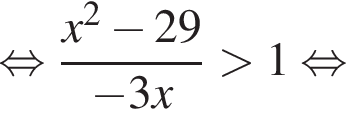
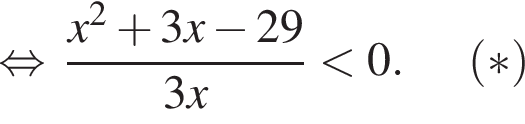
Найдем корни числителя:
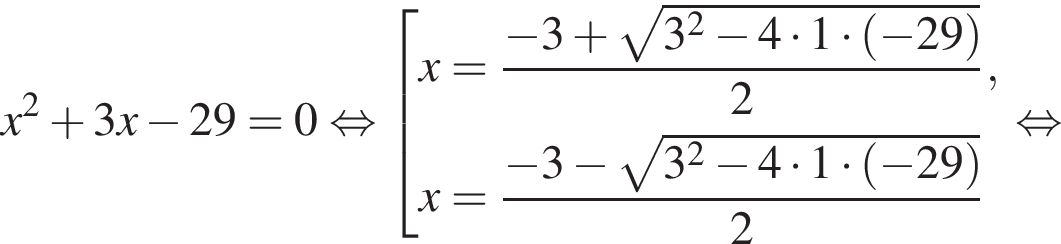
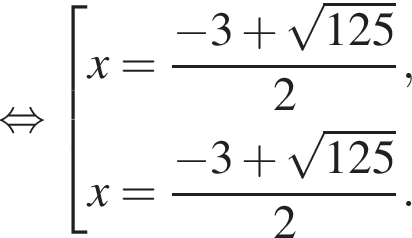
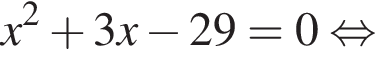
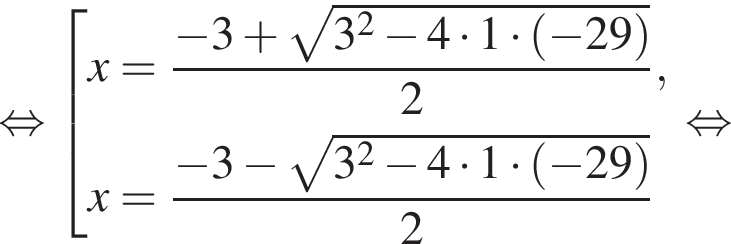
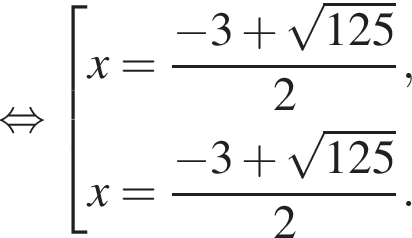
Методом интервалов получаем решения неравенства (⁎):
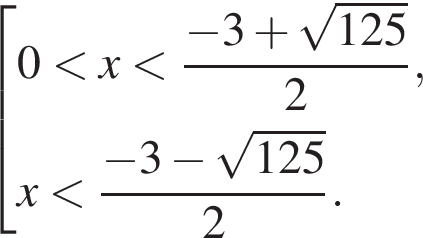
Найдем наибольшее целое отрицательное и наибольшее целое положительное решения исходного неравенства. Для этого выполним оценки:
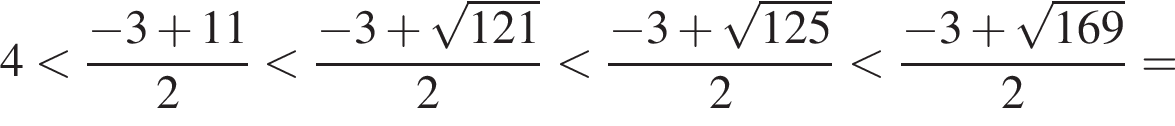
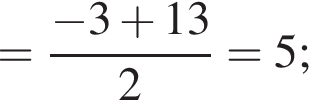
![]()
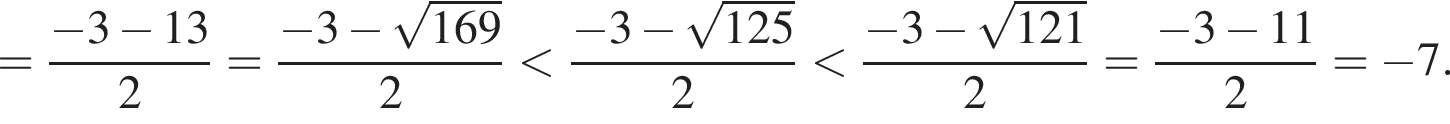
В силу полученных оценок наибольшим отрицательным решением является число −8, а наибольшим положительным — число 4. Их произведение равно −32.
Ответ: −32.
Ответ: -32
1610
-32
Сложность: III
Классификатор алгебры: 4\.2\. Неравенства первой и второй степени относительно показательных функций
Методы алгебры: Замена переменной
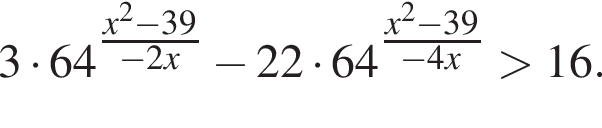
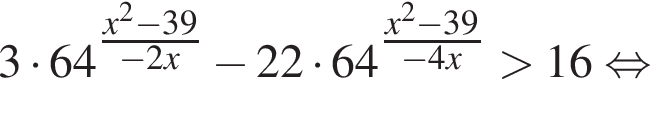
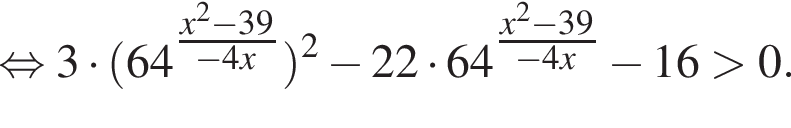
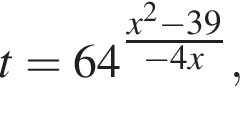 тогда имеем:
тогда имеем: